Die Technik der Sky-Dweller Teil 2: Jahreskalender (SAROS-System)

[Prof. Rolex]

Liebe Rolex-Fans,
nachdem im ersten Teil der kleinen Technik-Reihe zur Sky-Dweller die Ring-Command-Lünette beschrieben wurde ( Die Technik der Sky-Dweller Teil 1: Ring-Command-Lünette), wird in dem vorliegenden zweiten Teil auf den Jahreskalender mit SAROS-System eingegangen.

Die Sky-Dweller ist die erste Rolex mit einem Jahreskalender, wobei sich dessen Konstruktion erheblich von den bereits am Markt erhältlichen Jahreskalendern unterscheidet. Jahreskalendermechanismen bestehen üblicherweise aus einem komplexen System von Hebeln, Federn und Nocken, wobei je nach Filigranheit der Konstruktion die Robustheit manchmal etwas leidet. Rolex hingegen hat einen mechanisch sehr einfachen Jahreskalendermechanismus entwickelt (SAROS-System) welcher zusätzlich zu dem normalen Datumsmechanismus lediglich 4 weitere Zahnräder benötigt. Hinter dieser schon beinahe „genial“ einfachen Lösung steckt allerdings eine umso kompliziertere Theorie, wobei der Trick in der geschickten Wahl der Übersetzungsverhältnisse liegt.


Der Jahreskalender im Vergleich zu anderen Datumsanzeigen:
Betrachten wir zunächst einen Jahreskalender im Vergleich zur normalen Datumsanzeige und zum ewigen Kalender.

Normale Datumsanzeige:
Die Datumsanzeige springt alle 24 h um jeweils einen Tag weiter und dies ohne Berücksichtigung unterschiedlicher Monatslängen. Daher muß an den Monaten mit weniger als 31 Tagen eine manuelle Korrektur der Datumsanzeige vorgenommen werden. Eine normale Datumsanzeige muß also 5-mal im Jahr (Februar, April, Juni, September, November) korrigiert werden.

Jahreskalender:
Die Datumsanzeige springt alle 24 h um entweder einen (alle Tage außer 30.4, 30.6., 30.9. und 30.11.) oder zwei Tage (nur am 30.4, 30.6., 30.9. und 30.11.) weiter. Ein Jahreskalender berücksichtigt die Monate mit 30 Tagen, nicht jedoch den 28. bzw. den 29. Februar. Ein Jahreskalender muß also 1-mal im Jahr (Februar) korrigiert werden.

Ewiger Kalender:
Die Datumsanzeige springt alle 24 h um entweder einen (alle Tage außer 28.2., 29.2., 30.4, 30.6., 30.9. und 30.11.), zwei Tage (nur am 30.4, 30.6., 30.9. und 30.11.), drei Tage (29.2. in Schaltjahren) oder vier Tage (28.2. in Normaljahren) weiter. Ein ewiger Kalender berücksichtigt alle unterschiedlichen Monatslängen innerhalb eines 4-jährigen Zyklus (3 Normaljahre plus 1 Schaltjahr). Ein ewiger Kalender muß also nicht korrigiert werden.

Achtung: Die sogenannte Säkularjahrregel (Säkularjahre sind keine Schaltjahre, es sei denn die Jahreszahl ist durch 400 teilbar, deshalb ist 2000 ein Schaltjahr, die Jahre 1800, 1900 und 2100 aber nicht) berücksichtigt auch der ewige Kalender nicht. Meines Wissens nach hat nur Svend Andersen bisher eine Armbanduhr entwickelt, die auch die Säkularjahrregel berücksichtigt, den sogenannten säkularen ewigen Kalender.


Die Funktion des Saros-Systems:
Wie bereits erwähnt, handelt es sich bei dem SAROS-System um ein sehr einfaches System zur Realisierung eines Jahreskalenders. Dazu wird ein einfaches Planetengetriebe verwendet, dessen Sonnenrad feststeht und das von der Datumsscheibe angetriebene Planetenrad über das Sonnenrad abwälzt. Die Bahnkurve eines beliebigen Punktes auf dem Planetenrad folgt dann einer sogenannten Epizykloide, mit deren Theorie wir uns später noch genauer beschäftigen, da sie die Grundlage für die Wahl des „richtigen“ Übersetzungsverhältnisses ist.

Nachfolgend eine kleine Animation, die das Grundprinzip des Getriebes oder wie Rolex es nennt, des „SAROS-Systems“ verdeutlicht:


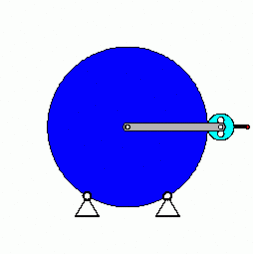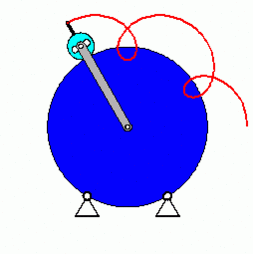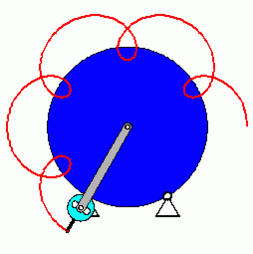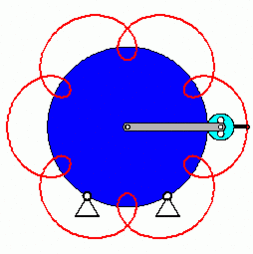
(Quelle: tm-aktuell.de)

Die Bahnkurve (rote Linie) eines Punktes am Planetenrad folgt dabei einer Epizykloide.

Und hier sehen wir nun das SAROS-System innerhalb des Datumsmechanismus, wie er in der Sky-Dweller verwendet wird:


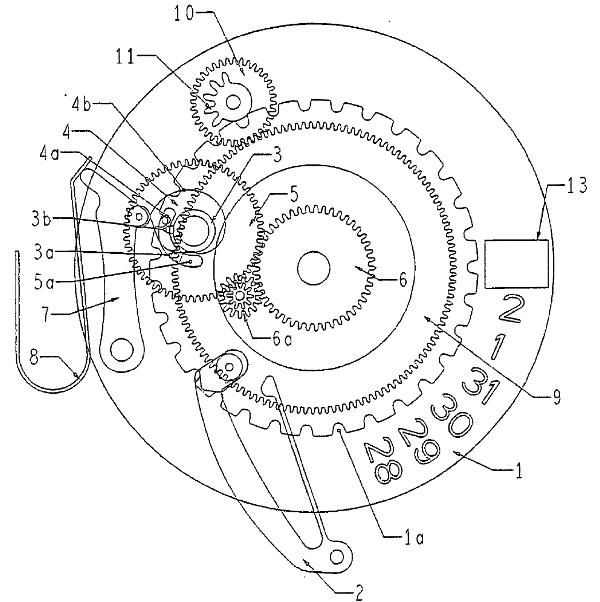
(Quelle: EP1596261)

Das mit der Datumsscheibe (1) verbundene Planetenrad (10) läuft um das feststehende Sonnenrad (9). Das Planetenrad verfügt über ein weiteres kleines Ritzel (11) welches fest mit dem Planetenrad verbunden ist. Dieses Ritzel verfügt über nur 5 Zähne, die je nach Lage der Datumscheibe und des damit verbundenen Planetenrades im Eingriff mit dem Schaltfinger (3b) des Datumsschaltrades (3) stehen. Dieser Schaltfinger wird nur bei den Monaten mit weniger als 31 Tagen am jeweils 30. Tag von den Zähnen des Ritzels betätigt und bewirkt einen zusätzlichen Sprung der Datumsscheibe, so daß das Datum direkt von „30“ auf „1“ springt.

Nur das Sonnenrad (9), das Planetenrad (10) mit dem Ritzel (11) und dem speziellen Datumsschaltrad (3) mit zwei Schaltfingern (3a) und (3b) sind dabei Teile des SAROS-Systems. Die übrigen Teile gehören zu dem normalen Datumsmechanismus, der in jeder Rolex mit Datum Verwendung findet, allerdings hat das Datumsschaltrad (3) dann nur einen Schaltfinger (3a). Die Anzahl zusätzlicher Teile für den Jahreskalender ist also tatsächlich auf ein Minimum reduziert.

Betrachen wir nun die Funktion etwas genauer und auf das SAROS-System beschränkt:


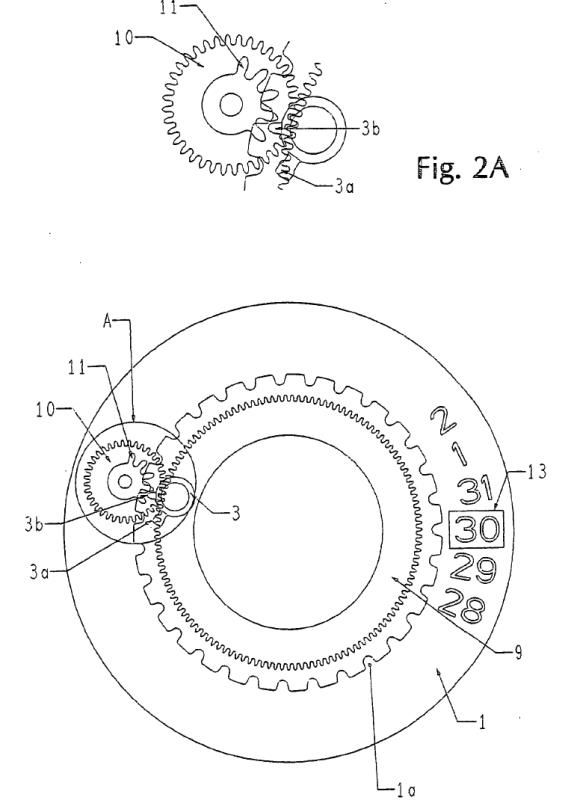
(Quelle: EP1596261)

Hier sehen wir die Teile des SAROS-Systems wie sie am 30. November zueinander positioniert sind. Die Datumsanzeige (13) zeigt „30“, das über die Datumssscheibe (1) angetriebene Planetenrad (10) liegt gegenüber dem Datumsschaltrad (3) und ein Zahn des Ritzels (11) ist im Eingriff mit dem zweiten Schaltfinger (3b). Der Datumsmechanismus ist noch nicht ausgelöst worden.

Achtung, jetzt geht es los! Es ist Mitternacht des 1. Dezember und der Datumsmechanismus ist ausgelöst worden:


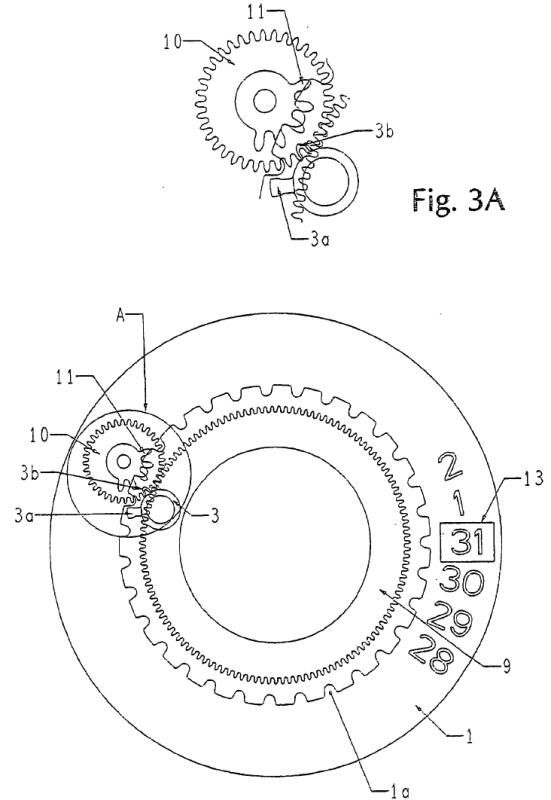
(Quelle: EP1596261)

Zunächst wird durch den ausgelösten Datumsmechanismus die Datumsscheibe (1) gedreht, wodurch sich gleichzeitig auch das Planetenrad (10) mit dem Ritzel (11) bewegt. Da ein Zahn des Ritzels aber mit dem zweiten Schaltfinger (3b) im Eingriff ist, wird das Datumsschaltrad (3) um eine Position weiterbewegt und die Datumsanzeige zeigt kurzzeitig die „31“ bis über den immer noch freigegebenen Datumsmechanismus mit dem ersten Schaltfinger (3a) der ganz normale tägliche Datumswechsel erfolgt. Ergebnis: Die Datumsanzeige ist von „30“ direkt auf „1“ gesprungen.

Natürlich erfolgt der Wechsel von der „30“ über „31“ auf die „1“ in Bruchteilen einer Sekunde und ist für das bloße Auge kaum wahrnehmbar, so wie wir es von Rolex (mit Ausnahme einiger älterer Kaliber) gewöhnt sind.

Wie sieht aber nun die Positionierung des Planetenrades und des Ritzels beispielsweise am 30. März aus, wo ja kein zweifacher Datumssprung erforderlich ist? Das folgende Bild zeigt das SAROS-System am 30. März:


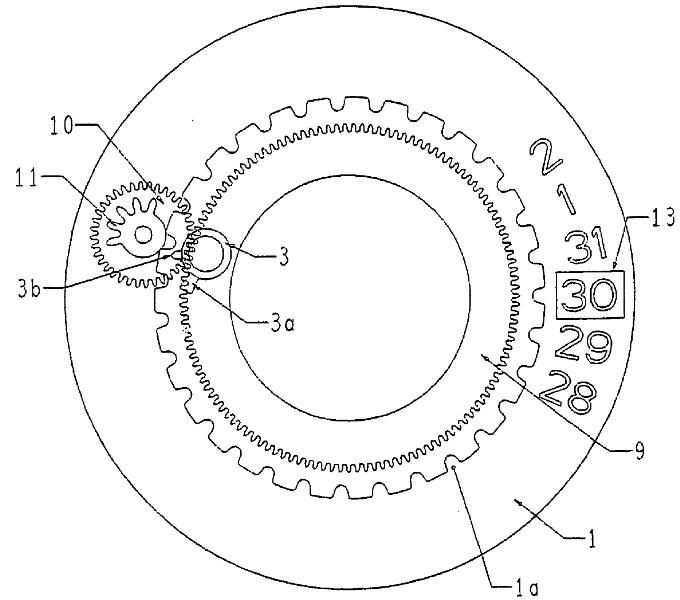
(Quelle: EP1596261)

Wie an jedem 30. Tag liegt auch hier wieder das Planetenrad (10) gegenüber dem Datumsschaltrad (3). Aber im Gegensatz zu den Monaten mit weniger als 31 Tagen ist nun keiner der Zähne des Ritzels (11) im Eingriff mit dem zweiten Schaltfinger (3b). Es erfolgt also ein ganz normaler Datumswechsel auf die „31“.

Das mechanische Grundprinzip ist also relativ einfach, der Trick liegt in der Auslegung des Planetengetriebes. Die Übersetzungsverhältnisse sind so zu wählen, daß folgende Bedingungen gewährleistet sind:

1. Zeigt die Datumsscheibe „30“ so muß die Position des Planetenrades immer gegenüber dem Datumsschaltrad liegen.
2. Nur an Monaten mit weniger als 31 Tagen darf ein Zahn des Ritzels im Eingriff mit dem zweiten Schaltfinger sein.
3. Nach 12 Umläufen (= 1 Jahr) der Datumsscheibe muß sich das gesamte System wieder in der Ausgangsposition befinden.

Rolex ist es tatsächlich gelungen Übersetzungsverhältnisse zu finden, die die obigen Bedingungen erfüllen und so einen mechanisch sehr einfachen und nur aus wenigen zusätzlichen Teilen bestehenden Jahreskalender zu entwickeln. Die Theorie hierzu ist allerdings wesentlich komplexer als die Mechanik des SAROS-Systems selbst.


Zur Theorie des SAROS-System:
Um die Theorie hinter dem SAROS-System genauer zu beleuchten, müssen wir uns zunächst mit der Theorie der Epizykloiden beschäftigen.

Hier noch einmal die bereits oben gezeigte Animation, die die Enstehung einer Epizykloide durch das Abwälzen eine Planetenrades auf einem festehenden Sonnenrad zeigt:


(Quelle: tm-aktuell.de)

Die Bahnkurve (rote Linie) eines Punktes am Planetenrad folgt dabei einer Epizykloide.

Für Epizykloiden gelten folgende Gesetzmäßigkeiten:

1. Ist das Übersetzungsverhältnis von Sonnenrad zu Planetenrad ganzzahlig, so schließt sich die Epizykloide bereits nach einem Stegumlauf. Dies ist in der obigen Animation der Fall.

2. Ist das Übersetzungsverhältnis von Sonnenrad zu Planetenrad eine rationale Zahl, so schließt sich die Epizykloide erst nach mehreren Umläufen. Dabei wird das Übersetzungsverhältnis als Bruch mit natürlichen Zahlen im Nenner und Zähler geschrieben, bis sich der Bruch nicht weiter kürzen läßt. Der Nenner gibt dann die Anzahl der Stegumläufe an bis sich die Epizykloide schließt und wieder in der Ausgangsposition ist.

3. Ist das Übersetzungsverhältnis von Sonnenrad zu Planetenrad eine irrationale Zahl, so schließt sich die Epizykloide nie und gerät nie wieder in die Ausgangsposition.

Aha, hier erhalten wir bereits einen ersten Hinweis auf die erforderliche Zähnezahl des Planetenrades für das SAROS-System. Damit das SAROS-System nach einem Jahr (=12 Umläufe der Datumsscheibe und des Planetenrades) wieder in der Ausgangsposition angelangt ist, muß die Zähnezahl des Planetenrades gemäß Fall 2 ein Vielfaches von 12 (12, 24, 36, 48, etc.) sein.

Gut, das ist doch schon etwas, aber was ist mit dem Sonnenrad? Wieviel Zähne muß dieses Rad aufweisen? Und wie müssen die Zähne auf dem Ritzel angeordnet werden, um nur an Monaten mit weniger als 31 Tagen einen zusätzlichen Datumssprung auszulösen? Und ist es tatsächlich möglich die Zähne des Ritzels, wie in den obigen Zeichnungen zu sehen, nebeneinander anzuordnen?

Rolex gibt in seiner Patentschrift eine empirisch (!) ermittelte Formel für die Anzahl der Zähne des Sonnenrades an:


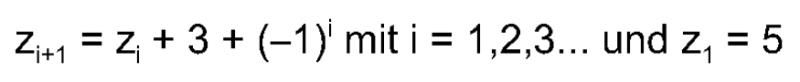
(Quelle: EP1596261)

Diese „Rolex-Saros-Formel“ sieht auf den ersten Blick mysteriös aus, daher habe ich die Formel in einer Excel-Tabelle programmiert und auch die bereits bekannte Zähnezahl des Planetenrades (Vielfaches von 12) mit einbezogen :



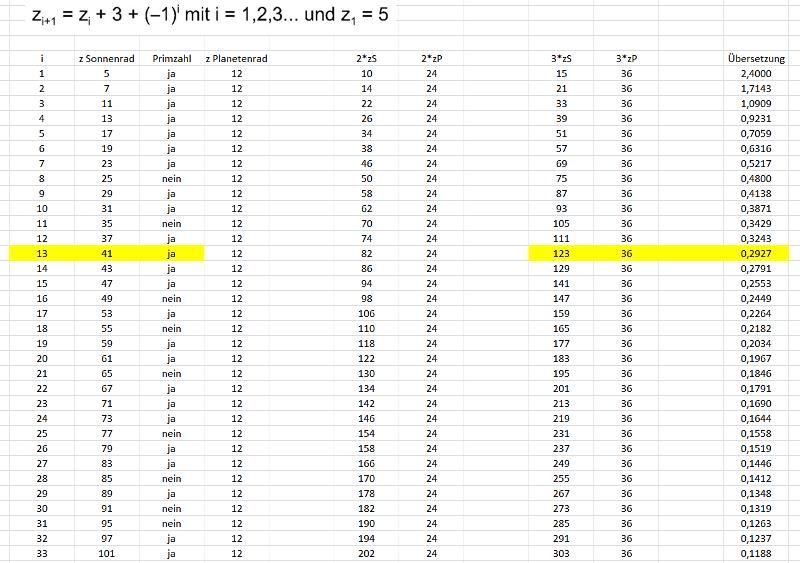
Hiermit erhalten wir eine Tabelle der zulässigen Zähnepaarungen (=Übersetzungen) des SAROS-Systems. Die gelb markierte Paarung gibt die in der Patentschrift verwendete Zahnradpaarung 123/36 an, die vermutlich auch tatsächlich im SAROS-System der Sky-Dweller verwendet wird. Nach 12 Umläufen der Datumsscheibe (=1 Jahr) und des Planetenrades ist das System mit einer Übersetzung von 123/36 wieder in der Ausgangsposition (123/36, gekürzt auf 41/12, weiteres Kürzen nicht möglich, da 41=Primzahl => 12 Umläufe zur Ausgangsposition).

Wie sieht aber denn nun die Epizykloide eines Punktes (zum Beispiel eine Zahnes des Ritzels) auf dem Planetenrad aus? Ist tatsächlich mit den nach der „Rolex-Saros-Formel“ gewonnenen Übersetzungsverhältnissen gewährleistet, daß sich nur in Monaten mit weniger als 31 Tagen ein Zahn des Ritzels im Eingriff mit dem zusätzlichen Schaltfinger befindet?

Um diese Frage zu beantworten müssen wir (leider) noch etwas tiefer in die Epizykloiden-Theorie einsteigen. Dazu habe ich die Parameterdarstellung der Epizykloide in einer Excel-Anwendung programmiert und kann so jeden Punkt auf einer beliebigen Epizykloide berechnen:



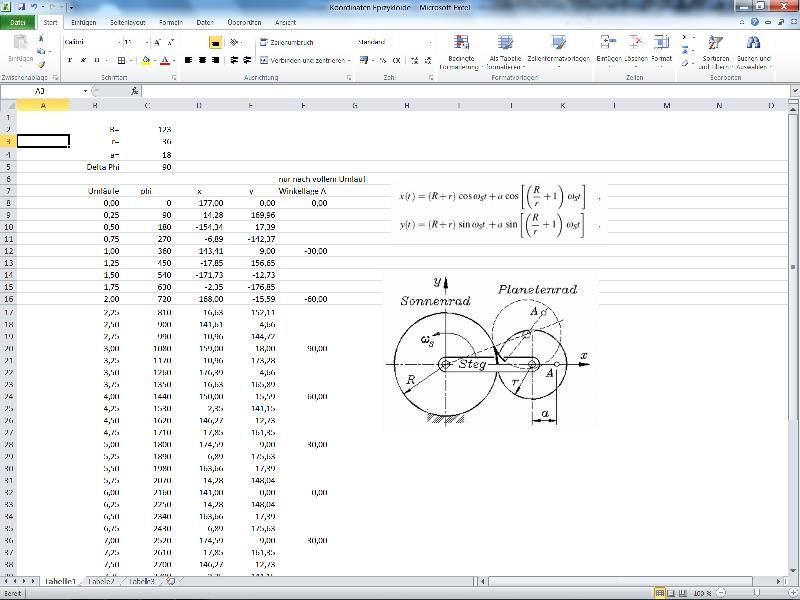
Die obige Tabelle zeigt bereits die Koordinaten der SAROS-Epizykloide mit einem Übersetzungsverhältnis von 123/36 für einen Referenzpunkt im Abstand von r/2 auf dem Planetenrad mit Winkelschritten von jeweils 90°.

Ein solcher „Zahlenfriedhof“ ist natürlicherweise nicht sehr plakativ, daher nachfolgend eine graphische Darstellung aus dem Excel-Programm des ersten Planetenradumlaufes im Januar:



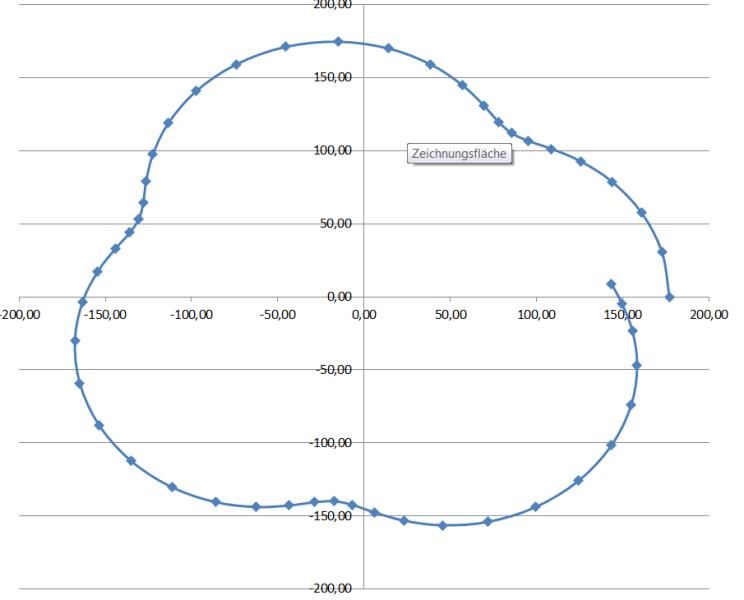
Es zeigt sich, daß der Referenzpunkt nach einem Umlauf an einer anderen Stelle liegt, die gegenüber der Ausgangsposition um genau 150° nach links gedreht ist. Diese Winkeldifferenz gilt übrigens auch für alle anderen Punkte auf dem Planetenrad und somit auch für die Zähne des Ritzels, das den zusätzlichen Schaltfinger zur Datumskorrektur betätigt.

Und hier der zweite Umlauf im Februar:



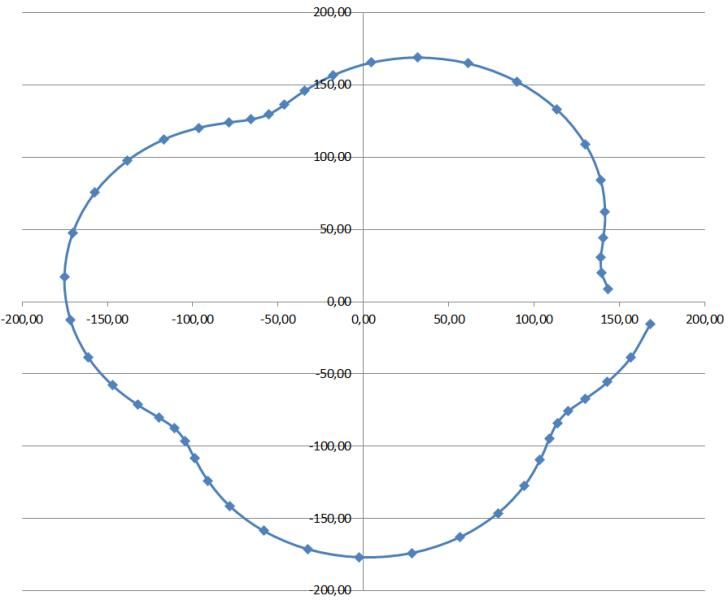
Eneut ist der Referenzpunkt nach dem zweiten Umlauf an einer anderen Stelle, die allerdings gegenüber dem Endpunkt des ersten Umlaufes erneut um 150° nach links gedreht ist.

Aha, wir kommen der Lösung näher: Offensichtlich ist der Referenzpunkt (und damit auch jeder andere Punkt auf dem Planetenrad) nach jedem Umlauf um 150° nach links gedreht. Damit müsste sich ja auch eine Reihenfolge der Zähne am Ritzel errechnen lassen, um nur an Monaten mit weniger als 31 Tagen einen Zahn im Eingriff des zusätzlichen Schaltfingers zu haben. Liegen die Zähne bzw. die Monate mit weniger als 31 Tagen dann tatsächlich nebeneinander?

Lassen wir nun die obige Excel-Tabelle mit der SAROS-Epizykloide und Winkelschritten von von jeweils 360° (=1 Monat) über zwölf Umläufe (=1 Jahr) berechnen und dies graphisch darstellen, so ergibt sich ein wirklich erstaunliches Ergebnis:



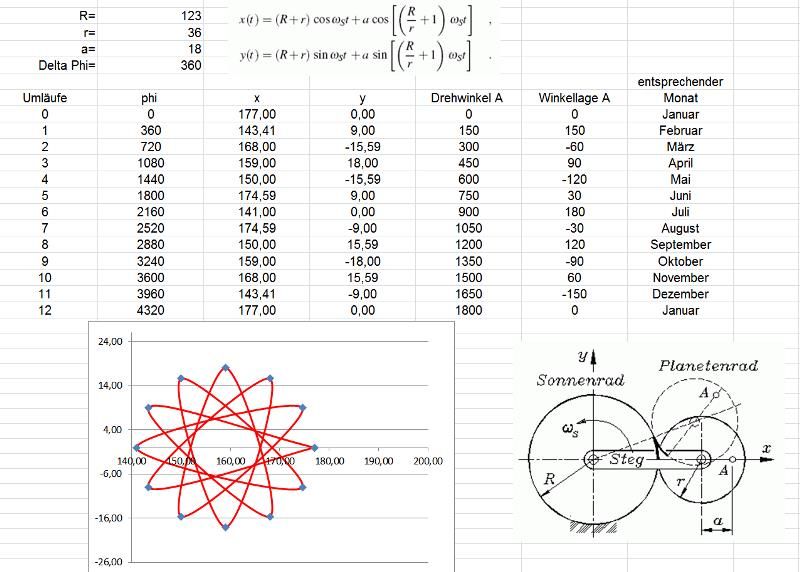
Wir erhalten tatsächlich eine Epizykloide, die uns die erforderliche Anordnung der Zähne auf dem Ritzel zur Betätigung des zusätzlichen Schaltfingers angibt. Hier noch einmal diese spezielle Epizykloide mit Angabe der Laufrichtung und der Reihenfolge der Monate im Ablauf während 12 Umläufen (=1Jahr):



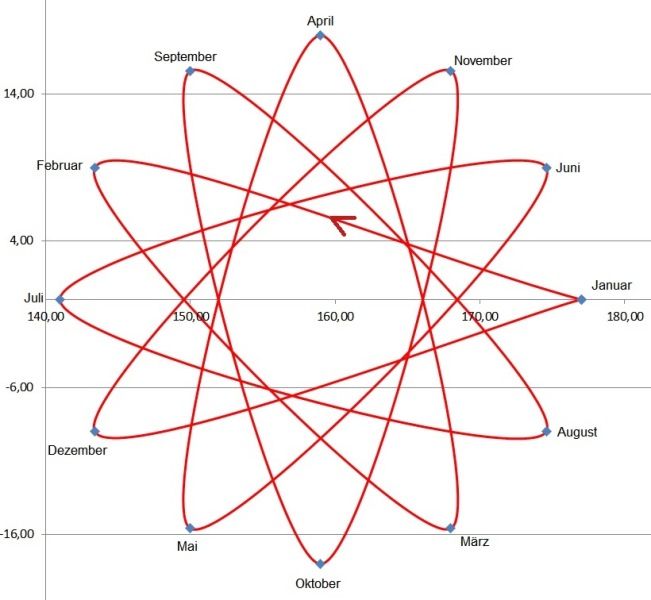
Es ist beinahe unglaublich, aber die 5 Monate mit weniger als 31 Tagen (Februar, September, April, November, Juni) liegen wirklich alle nebeneinander. Daher hat das erforderliche Ritzel zur Steuerung des zusätzlichen Datumssprungs auch tatsächlich 5 aufeinanderfolgende Zähne und dann keine weiteren Zähne.

Übrigens hat Rolex höchstwahrscheinlich in der Sky-Dweller auf den fünften Zahn für den Februar verzichtet, da im Februar ohnehin bereits am 28. oder 29. manuell korrigiert werden muß.

So, für heute habe ich Euch genug mit Formeln, Epizykloiden und Planetenübersetzungen malträtiert. Zusammenfassend fällt mir zum SAROS-System in Anlehnung an einen älteren Werbespruch aus den 80er Jahren ein:

It´s not a trick, it´s a Rolex!

Solltet Ihr übrigens die Monatsanzeige der Sky-Dweller in diesem Beitrag vermisst haben, die Monatsanzeige ist Bestandteil eines weiteren Rolex-Patentes und wird dann im 3. Teil der Technik-Reihe zur Sky-Dweller beschrieben. Bis dahin……

Viele Grüße
Matthias

[OrangeHand]

Sehr interessant Matthias.
Da steckt eine Menge Arbeit in Deiner Erläuterung.
Ich glaube ich bin da einigermassen durchgestiegen.

Herzlichen Dank




Eine Frage hätte ich: Bist Du Dir hierbei sicher?

Übrigens hat Rolex höchstwahrscheinlich in der Sky-Dweller auf den fünften Zahn für den Februar verzichtet, da im Februar ohnehin bereits am 28. oder 29. manuell korrigiert werden muß.

Technisch "pfiffig" wäre das Auslassen des 5. Zahnes am Monatsplanetenrad (11) durchaus.

Aber der im Patent EP1596261 B1 beanspruchte Jahreskalendermechanismus definiert im Hauptanspruch ganz explizit, dass das Monatsplanetenrad (11) "fünf Antriebszähne" aufweisen muss.

Der Verzicht auf den Antriebszahn für Februar würde somit nicht mehr unter den Schutz des Patents EP1596261 B1 fallen. (Und solch ein Gegenstand ist dank dieses Thread auch nicht mehr Patentfähig... )




Übrigens

Ulysse Nardin hat in ihrem Patent EP1351104 B1 vom November 2008 ein ähnliches Monatsplanetenrad beschrieben. Dieses weist 12 Antriebszähne auf, wobei 7 davon kurz sind, und 5 davon radial länger geformt sind. Der Zweck der 5 längeren Antriebszähne entspricht dem, was oben erläutert wurde.

[alicia]

ich hab mich ein bisschen schwer getan, aber zumindest größtenteils konnte ich folgen ...ganz große Klasse - vielen Dank

[AndreasS]

Super Arbeit, Matthias.

Sehr gut erklärt, wie immer.

[WUM]

geht mir nicht anders... heftige Lektüre.....herzlichen Dank


Gruss


Wum

[Bullit]

Einsame Klasse, vielen Dank!

Am erstaunlichsten finde ich folgende von dir erwähnte Tatsache: "Die Theorie hierzu ist allerdings wesentlich komplexer als die Mechanik des SAROS-Systems selbst."

Hätte ich nie gedacht.

Gruß

Erik

[Prof. Rolex]

ich hab mich ein bisschen schwer getan, aber zumindest größtenteils konnte ich folgen ...ganz große Klasse - vielen Dank

Liebe Anna,
vielen Dank für Deinen freundlichen Kommentar. Ich gebe zu, daß auch mir während der Beschäftigung mit den theoretischen Grundlagen desöfteren der Kopf "geraucht" hat. Entspannung fand ich dann so manches mal in Deinen kaum zu übertreffenden Reiseberichten…..

Gruß
Matthias

[Prof. Rolex]

Eine Frage hätte ich: Bist Du Dir hierbei sicher?

Übrigens hat Rolex höchstwahrscheinlich in der Sky-Dweller auf den fünften Zahn für den Februar verzichtet, da im Februar ohnehin bereits am 28. oder 29. manuell korrigiert werden muß.

Technisch "pfiffig" wäre das Auslassen des 5. Zahnes am Monatsplanetenrad (11) durchaus.

Aber der im Patent EP1596261 B1 beanspruchte Jahreskalendermechanismus definiert im Hauptanspruch ganz explizit, dass das Monatsplanetenrad (11) "fünf Antriebszähne" aufweisen muss.

Der Verzicht auf den Antriebszahn für Februar würde somit nicht mehr unter den Schutz des Patents EP1596261 B1 fallen. (Und solch ein Gegenstand ist dank dieses Thread auch nicht mehr Patentfähig... )

Lieber Frank,
es gibt zwei Indizien, die auf die Verwendung eines Ritzels mit nur vier anstatt fünf Zähnen hinweisen:

1. In der Pressemappe zur Sky-Dweller und auf der Rolex-Homepage ist in Bezug auf das SAROS-System u.a. zu lesen: „Dieses Planetenrad ist mit vier Fingern (sie symbolisieren den Mond) für jeden der vier 30-tägigen Monate (April, Juni, September und November) ausgestattet“.

2. Ebenfalls auf der Rolex-Homepage ist ein kleine Animation zum SAROS-System zu sehen und auch dort ist nur ein vierzähniges Ritzel zu erkennen.

Mit den daraus eventuell resultierenden patentrechtlichen Umständen kenne ich mich allerdings nicht so sehr aus, das ist eher etwas für Dich…..

Gruß
Matthias

[Daytona]

[superolli]

Ich hab' mich da jetzt wirklich durchgearbeitet.
Respekt und Danke.

[husi]

Lieber Matthias, ganz herzlichen Dank.

Das Tragen der Uhr ist glücklicherweise einfacher als Deinen exzellenten Beitrag bis ins letzte Detail zu verstehen.

[Vanessa]

Sehr geil, Matthias, nach einer Stunde habe ich es jetzt auch kapiert. Oder? Die Frage ist nur- wie kommt man auf die Formel? Back-Engineering vom Ergebnis?

[Mr Mille Gauss]

Hallo,

1 weiss ich nach dem Montag sicher........es funkt Hammerg..... und sehr überzeugend!
Haptik und Funktion sind ohne Fehl und Tadel.

[Bildverarbeiter]

Vielen Dank! Sehr gut aufbereitet, sehr verständlich..

[Deralex]

Deine Erklärungen sind ganz große Klasse, danke dafür

[Mücke]

Vielen Dank für's Bildungsfernsehen.

[Hunter99]

Klasse, wie hast du geschrieben "genial einfach" Rolex ist Apple der Uhrenwelt :-)

[ehemaliges mitglied]

Von fünf Daumen, sechs Daumen nach oben



Klasse Beschreibung!

[Duc Loan]

1+ mit

[intimeout]

Danke, genialer Beitrag.
Danke für Deine Mühen.